【算法基础】前缀树

算法
,

前缀树也称为字典树、Trie树，优点在于利用字符串的公共前缀来减少查询时间，常被搜索引擎用于文本词频统计。

前缀树构建过程

以字符串“abc”，“abd”，“bce”，“abcd”为例，前缀树构建过程如下图所示：

  • 每个节点记录经过当前节点的字符串数量p和是否是字符串结尾e
  • 每条线段表示字符

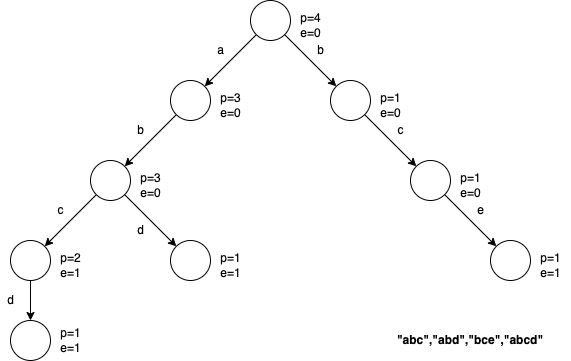
image

前缀树实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
public static class Node {
    public int pass;
    public int end;
    public Node[] nexts;

    public Node() {
        pass = 0;
        end = 0;
        nexts = new Node[26];
    }
}

public static class Trie {
    public Node root;

    public Trie() {
        root = new Node();
    }

    // 插入字符串word
    public void insert(String word) {
        if (word == null) {
            return;
        }

        char[] chs = word.toCharArray();

        Node node = root;
        node.pass++;
        int path = 0;
        for (int i = 0; i < chs.length; i++) { // 从左往右遍历字符
            path = chs[i] - 'a'; // 字符
            if (node.nexts[path] == null) { // 当前字符对应的node不存在就新建
                node.nexts[path] = new Node();
            }
            node = node.nexts[path]; // 指针移动到当前node
            node.pass++; // 当前node pass + 1
        }
        node.end++; // 最后一个字符对应的node end + 1
    }

    // 删除字符串word
    public void delete(String word) {
        if (search(word) != 0) { // 不存在直接跳过
            char[] chs = word.toCharArray();
            Node node = root;
            node.pass--; // root pass直接-1
            int path = 0;
            for (int i = 0; i < chs.length; i++) {
                path = chs[i] - 'a';
                if (--node.nexts[path].pass == 0) { // 如果字符pass-1后是0，直接设为空结束
                    node.nexts[path] = null;
                    return;
                }
                node = node.nexts[path];
            }
            node.end--;
        }
    }

    // 查找word加入过几次
    public int search(String word) {
        if (word == null) {
            return 0;
        }

        char[] chs = word.toCharArray();
        Node node = root;
        int index = 0;
        for (int i = 0; i < chs.length; i++) {
            index = chs[i] - 'a';
            if (node.nexts[index] == null) {
                return 0;
            }
            node = node.nexts[index];
        }
        return node.end;
    }

    // 查找以pre作为前缀的字符串数量
    public int prefixNumber(String pre) {
        if (pre == null) {
            return 0;
        }
        char[] chs = pre.toCharArray();
        Node node = root;
        int index = 0;
        for (int i = 0; i < chs.length; i++) {
            index = chs[i] - 'a';
            if (node.nexts[index] == null) {
                return 0;
            }
            node = node.nexts[index];
        }
        return node.pass;
    }
}