【算法基础】排序算法（总）

算法
,

排序算法分析

执行效率

排序算法执行效率分析从以下几个方面来衡量：

  • 最好情况、最坏情况、平均情况时间复杂度
  • 时间复杂度的系数、常数 、低阶
  • 比较次数和交换（或移动）次数

内存消耗

算法的内存消耗可以通过空间复杂度来衡量。针对排序算法的空间复杂度，引入原地排序（Sorted in place）概念，特指空间复杂度是 O(1) 的排序算法。

稳定性

排序算法的稳定性：如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变则稳定，否则不稳定。

冒泡排序（Bubble Sort）

冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较，看是否满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少一个元素移动到它应该在的位置，重复 n 次，就完成了 n 个数据的排序工作。

动画演示

image

代码示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
public static void bubbleSort(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }
    int n = arr.length;

    // 0 - n
    // 0 - n-1
    // 0 - n-2
    for (int end = n - 1; end >= 0; end--) {

        // 提前退出冒泡循环的标志位
        boolean flag = false;

        // 0, 1
        // 1, 2
        // 2, 3
        for (int second = 1; second <= end; second++) {
            if (arr[second - 1] > arr[second]) {
                // 表示有数据交换
                flag = true;
                swap(arr, second - 1, second);
            }
        }

        // 没有数据交换，提前退出
        if (!flag) {
            break;
        }
    }
}

public static void swap(int[] arr, int i, int j) {
    int tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
}

复杂度分析

时间复杂度：

  • 最好情况：要排序的数据已经是有序的了，只需要进行一次冒泡操作，时间复杂度O(n)，例如：“1,2,3,4,5,6”
  • 最坏情况：要排序的数据刚好是倒序排列的，需要进行 n 次冒泡操作，时间复杂度为 O(n^2)，例如：“6,5,4,3,2,1”
  • 平均情况：O(n^2)

空间复杂度：

冒泡排序只涉及相邻数据交换操作，时间复杂度为O(1)，是一个原地排序算法。

插入排序（Insertion Sort）

插入排序包含元素比较和元素移动两种操作。当需要将一个数据 a 插入到已排序区间时，需要拿 a 与已排序区间的元素依次比较大小，找到合适的插入位置。然后将插入点之后的元素顺序往后移动一位，再插入 a 元素。

动画演示

image

代码示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public static void insertSort(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }

    int n = arr.length;
    for (int i = 1; i < n; i++) {
        for (int j = i - 1; arr[j] > arr[j + 1] && j >= 0; j--) {
            swap(arr, j, j + 1);
        }
    }
}

public static void swap(int[] arr, int i, int j) {
    int tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
}

复杂度分析

时间复杂度：

  • 最好情况，数据有序，复杂度O(n)
  • 最坏情况，数据倒序，复杂度O(n^2)
  • 平均情况：O(n^2)

空间复杂度：

插入排序算法是原地排序算法，空间复杂度O(1)

选择排序（Selection Sort）

选择排序算法的实现思路有点类似插入排序，也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾。

动画演示

image

代码示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public static void selectSort(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }
    int n = arr.length;
    for (int i = 0; i < n; i++) {
        int minValueIndex = i;
        for (int j = i + 1; j < n; j++) {
            minValueIndex = arr[minValueIndex] > arr[j] ? j : minValueIndex;
        }
        swap(arr, i, minValueIndex);
    }
}

public static void swap(int[] arr, int i, int j) {
    int tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
}

复杂度分析

时间复杂度：

最好/最坏/平均情况下时间复杂度都为 O(n^2)

空间复杂度：

原地排序，复杂度O(1)

归并排序（Merge Sort）

归并排序：如果要排序一个数组，先把数组从中间分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并。

动画演示

image

代码示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
public static void mergeSort(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }

    process(arr, 0, arr.length - 1);
}

public static void process(int[] arr, int l, int r) {
    if (l == r) {
        return;
    }

    // 中点位置 (l+r)/2
    int mid = l + ((r - l) >> 1);

    // 二分后分别排序
    process(arr, l, mid);
    process(arr, mid + 1, r);

    // 合并已经排好序的两块数组
    merge(arr, l, mid, r);
}

public static void merge(int[] arr, int l, int mid, int r) {
    // 辅助数组
    int[] help = new int[r - l + 1];

    int i = 0;

    // 用两个指针分别指向[l,mid], (mid, r]
    int p1 = l;
    int p2 = mid + 1;

    // 正常范围, 依次比较, 小的放到辅助数组, 指针后移
    while (p1 <= mid && p2 <= r) {
        help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
    }

    // 如果p1没越界, p2越界, 把p1剩下的数拷贝到辅助数组
    while (p1 <= mid) {
        help[i++] = arr[p1++];
    }

    // 如果p2没越界, p1越界, 把p2剩下的数拷贝到辅助数组
    while (p2 <= r) {
        help[i++] = arr[p2++];
    }

    for (int j = 0; j < help.length; j++) {
        arr[l + j] = help[j];
    }
}

复杂度分析

时间复杂度：

根据Master公式，T(N) = 2 * T(N/2) + O(N)，a=2，b=2，d=1, log(b,a)==d，所以时间复杂度为O(N * logN)

最好情况、最坏情况，平均情况，时间复杂度都是 O(nlogn)。

空间复杂度：

空间复杂度O(n)。

快速排序（Quick Sort）

快速排序算法（Quicksort），简称为“快排”，利用的也是分治思想。

快排思想：(要排序数组中下标从 p 到 r 之间的一组数据)

  • 选择 p 到 r 之间的任意一个数据作为 pivot（分区点）。
  • 遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放到中间。

经过这一步骤之后，数组 p 到 r 之间的数据就被分成了三个部分，前面 p 到 q-1 之间都是小于 pivot 的，中间是 pivot，后面的 q+1 到 r 之间是大于 pivot 的。

根据分治、递归的处理思想，可以用递归排序下标从 p 到 q-1 之间的数据和下标从 q+1 到 r 之间的数据，直到区间缩小为 1，所有的数据都有序了。

动画演示

image

代码示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
// 随机快速排序
public static void quickSort(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }
    process(arr, 0, arr.length - 1);
}

public static void process(int[] arr, int l, int r) {
    if (l >= r) {
        return;
    }
    swap(arr, l + (int) (Math.random() * (r - l + 1)), r);
    int[] equalArea = partition(arr, l, r);
    process(arr, l, equalArea[0] - 1);
    process(arr, equalArea[1] + 1, r);
}

// 在arr[l...r]范围上, 对arr[r]做划分值
// 对于l...r范围, 小于arr[r]在左边, 等于在中间, 大于在右边
public static int[] partition(int[] arr, int l, int r) {
    // 小于区域右边界
    int lessR = l - 1;
    // 大于区域左边界
    int moreL = r;
    int index = l;
    while (index < moreL) {
        if (arr[index] < arr[r]) {
            // 如果小于, 跟小于区域右侧第一个值交换, 继续处理下一个值
            swap(arr, ++lessR, index++);
        } else if (arr[index] > arr[r]) {
            // 如果大于, 跟大于区域左侧第一个值交换, 交换完不需要移动index
            swap(arr, --moreL, index);
        } else {
            index++;
        }
    }
    // 交换大于区域左侧第一个值和目标arr[r]
    swap(arr, moreL, r);

    // 返回等于位置左右边界
    return new int[] { lessR + 1, moreL };
}

public static void swap(int[] arr, int i, int j) {
    int tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
}

复杂度分析

时间复杂度：

  • 最好、平均情况 O(nlogn)，每次分区操作，都能正好把数组分成大小接近相等的两个小区间
  • 最坏情况 O(n^2)，数组已有序排列

空间复杂度：O(nlogn)

堆排序（Heap Sort）

堆结构是用数组实现的完全二叉树结构，具体实现：优先级队列PriorityQueue。

完全二叉树中对于任意一个节点index=i，满足：

左孩子位置：2 * i + 1
右孩子位置：2 * i + 2
父节点位置：(i - 1) / 2

堆排序思想：

  1. 先让整个数组变成大根堆结构，建堆过程：
    a. 从上到下的方法，时间复杂度O(n*logn)
    b. 从下到上的方法，时间复杂度O(n)
  2. 把堆的最大值和堆末尾的值交换，减少堆的大小并重新调整堆，循环操作到堆的大小减小到0时，排序完成

大根堆：完全二叉树中如果每棵子树的最大值都在顶部就是大根堆。
小根堆：完全二叉树中如果每棵子树的最小值都在顶部就是小根堆。

动画演示

image

代码示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
// 堆排序额外空间复杂度O(1)
public static void heapSort(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }

    // 第一种方式构建大根堆，从上到下
    // O(N*logN)
    // for (int i = 0; i < arr.length; i++) {
    // heapInsert(arr, i);
    // }

    // 第二种方式构建大根堆，从下到上
    // O(N)
    for (int i = arr.length - 1; i >= 0; i--) {
        heapify(arr, i, arr.length);
    }

    int heapSize = arr.length;
    swap(arr, 0, --heapSize); // 交换0位置最大值到大根堆最后

    // O(N*logN)
    while (heapSize > 0) { // O(N)
        heapify(arr, 0, heapSize); // O(logN)
        swap(arr, 0, --heapSize); // O(1)
    }
}

// arr[index]位置的数，往上移动
public static void heapInsert(int[] arr, int index) {
    while (arr[index] > arr[(index - 1) / 2]) {
        swap(arr, index, (index - 1) / 2);
        index = (index - 1) / 2;
    }
}

// arr[index]位置的数，往下移动
public static void heapify(int[] arr, int index, int heapSize) {
    int left = index * 2 + 1; // 左孩子的下标
    while (left < heapSize) { // 下方还有孩子的时候
        // 两个孩子中，谁的值大，把下标给largest
        // 1) 只有左孩子，left -> largest
        // 2) 同时有左孩子和右孩子，右孩子的值 <= 左孩子的值，left -> largest
        // 3) 同时有左孩子和右孩子并且右孩子的值 > 左孩子的值， right -> largest
        int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;
        // 父和较大的孩子之间，谁的值大，把下标给largest
        largest = arr[largest] > arr[index] ? largest : index;
        if (largest == index) {
            break;
        }
        swap(arr, largest, index);
        index = largest;
        left = index * 2 + 1;
    }
}

public static void swap(int[] arr, int i, int j) {
    int tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
}

复杂度分析

时间复杂度：O(n*logn)，空间复杂度：O(1)。

计数排序（Count Sort）

对于有限数据范围的数据，利用一个相应大小的桶（从小到大对应每个数），对给定数组中每个值进行计数，完毕后从左到右每个数*n重新输出，完成排序。

动画演示

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public static void countSort(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }
    int max = Integer.MIN_VALUE;
    for (int i = 0; i < arr.length; i++) {
        max = Math.max(max, arr[i]);
    }
    int[] bucket = new int[max + 1];
    for (int i = 0; i < arr.length; i++) {
        bucket[arr[i]]++;
    }
    int i = 0;
    for (int j = 0; j < bucket.length; j++) {
        while (bucket[j]-- > 0) {
            arr[i++] = j;
        }
    }
}

复杂度分析

时间复杂度：O(n+k)，空间复杂度：O(k)。

基数排序（Radix Sort）

基数排序：准备一个大小为10的桶表示0-9，从个位开始，将每个数放到个位对应桶的位置里，然后按照先进先进输出，继续按照高位循环直到最大数最高位，相当于每次按照每位排序，到最高位后完成排序。

动画演示

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
// 只适用非负数
public static void radixSort(int[] arr) {
    if (arr == null || arr.length < 2) {
        return;
    }
    radixSort(arr, 0, arr.length - 1, maxbits(arr));
}

// 最大值位数
public static int maxbits(int[] arr) {
    int max = Integer.MIN_VALUE;
    for (int i = 0; i < arr.length; i++) {
        max = Math.max(max, arr[i]);
    }
    int res = 0;
    while (max != 0) {
        res++;
        max /= 10;
    }
    return res;
}

// arr[L..R]排序 , 最大值的十进制位数digit
public static void radixSort(int[] arr, int L, int R, int digit) {
    final int radix = 10;
    int i = 0, j = 0;
    // 有多少个数准备多少个辅助空间
    int[] help = new int[R - L + 1];
    for (int d = 1; d <= digit; d++) { // 有多少位就进出几次
        // 10个空间
        // count[0] 当前位(d位)是0的数字有多少个
        // count[1] 当前位(d位)是(0和1)的数字有多少个
        // count[2] 当前位(d位)是(0、1和2)的数字有多少个
        // count[i] 当前位(d位)是(0~i)的数字有多少个
        int[] count = new int[radix]; // count[0..9]
        for (i = L; i <= R; i++) {
            // 103 1 3
            // 209 1 9
            j = getDigit(arr[i], d);
            count[j]++; // count数组先按照位数计数
        }
        for (i = 1; i < radix; i++) {
            count[i] = count[i] + count[i - 1]; // count转变成累加和，累加和：大于等于当前数个数
        }
        for (i = R; i >= L; i--) { // 原数组从右往左遍历，利用累加和可以直接找到应该在的位置
            j = getDigit(arr[i], d);
            help[count[j] - 1] = arr[i]; // 当前数应该在的位置就是相应累加和-1的位置
            count[j]--; // 使用完之后把相应位置累加和-1
        }
        for (i = L, j = 0; i <= R; i++, j++) {
            arr[i] = help[j]; // 辅助空间 -> 原始数组
        }
    }
}

// 指定位，大小
public static int getDigit(int x, int d) {
    return ((x / ((int) Math.pow(10, d - 1))) % 10);
}

复杂度分析

时间复杂度：O(n*k)，空间复杂度：O(n+k)。

排序算法总结

  1. 不基于比较的排序，对样本数据有严格要求，不易改写
  2. 基于比较的排序，只要规定好两个样本怎么比大小就可以直接复用
  3. 基于比较的排序，时间复杂度极限是O(N*logN)
  4. 时间复杂度O(N*logN)，额外空间复杂度低于O(N)，并且稳定的基于比较的排序不存在
  5. 为了绝对的速度选快排，为了省空间选堆排，为了稳定性选归并

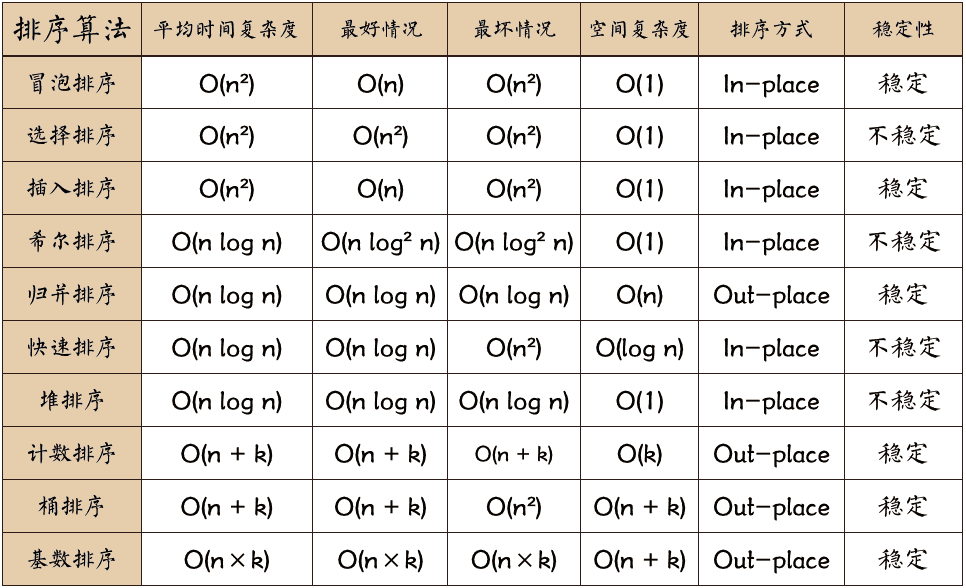
排序算法复杂度快查表

image